The basic critical period technique theory is applicable only to simple systems which consist of a single tank, with all the water demand downstream of the tank, such as depicted in the Simple Pipe Network Layout. The inflow capacity (Q) of the feeder pipe is constant, and depends on the pipe characteristics and available head between source and tank. The fluctuating nature of the demand downstream of the tank can be described by a peak factor curve (equation 1). The tank serves to equalize the differences between Q and the demand:
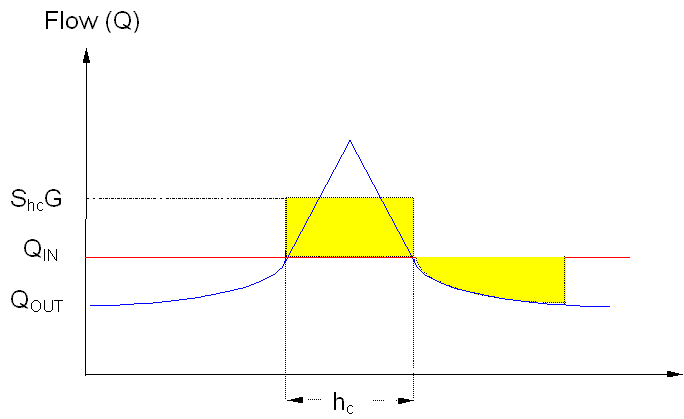
The balancing volume in the tank (V) required for a peak period of duration h hours is:

Substituting equation (1) into (2a):

A certain critical peak period (hc) would require a maximum V for the given Q.
This can be solved for by differentiation of equation (2):
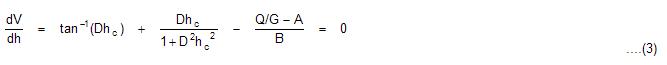
A solution of equation (3) will provide the value of the critical peak period hc. Equation (3) cannot be solved explicitly, and a numerical technique such as the bisection method or Newton Raphson iteration is required. Substituting the value for hc back into equation (2) gives the required balancing volume V for the tank.
Numerical example
Assume for the network in the “Simple Pipe Network” that Q = 300 m³/h, G = 125 m³/h and the demand peak factor curve shown in the Demand Fluctuations Graphs. From equation (3), to solve for hc:
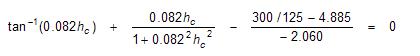
Therefore, hc = 10,51 hours (using the bisection method). Substitute this into equation (2) to determine the required balancing volume:

The time-saving potential of this technique is evident. Balancing volume is established through two equations, instead of a tedious time-step by time-step simulation procedure.